Fuente. Aula Fácil.2008
COEFICIENTE DE CORRELACIÓN INTERPRETACIÓN ESTADÍSTICA
Como
ya se ha planteado el grado de correlación mide la
intensidad de relación lineal, ya sea directa, inversa o inexistente
entre dos variables, se dice que es directa si tiene signo positivo, inversa de
signo negativo y nula cuando el valor sea aproximadamente igual a cero.
Existen diferentes métodos para calcular el
grado de correlación en este curso explicaremos el método en términos de
variaciones y simplificado de Kart Pearson.
El método de variaciones consiste en comparar el grado de desviación que se
presenta entre los valores observados, los proyectados y la media aritmética;
el de Kart Pearson lo resume en una ecuación determinada.
La
idea central radica en que si existe relación entre los valores de “Y”
observados con los valores de X, el grado de variación de la media
aritmética respecto a los “Y” estimados y los observados es mínima.
En
términos concretos se compara el porcentaje de la variación explicada (que se
origina entre los valores proyectados y la media), y la variación total (la
variación observada y la variación explicada) en cuyo caso refleja un
coeficiente que se encuentra entre el valor de -1 y 1.
De
manera funcional se mide:
Variación
total = variación no explicada + variación explicada
(Y
observada -media de Y) = (Y observada - Y estimada) + (Y
estimada - media de Y)
La
siguiente gráfica muestra las desviaciones a las que se hace referencia, el
valor de la media se representa por la variable Ψ y se obtiene de la suma
del valor observado dividido entre el total de observaciones, ![]() = ∑
Y / n.
= ∑
Y / n.

Para evitar valores negativos se debe llevar al cuadrado cada expresión, para
totalizar ese cálculo se realiza para cada uno de los puntos y luego se procede
a la suma en consecuencia
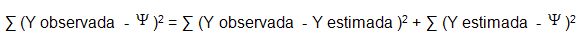
Como
el coeficiente de correlación es un porcentaje que explica el comportamiento de
la relación entre lo variación explicada y la variación total se calcula
mediante

Con esta ecuación se puede apreciar que en la medida que el valor de observado
sea igual al valor proyectado, el nivel de variación con la media será el
mismo, es decir que Y observado = Y estimado, si eso se cumple para cada uno de
los puntos las variaciones son inexistentes y por lo tanto
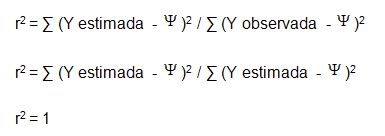
El
método de Pearson no es más que aplicar la siguiente ecuación
![]()