Fuente. Aula Fácil.2008
FUNCIÓN CUADRÁTICA
La
forma funcional de cada modelo econométrico depende en alguna parte por su
forma gráfica, es decir que al reflejar en un esquema bidimensional
se puede apreciar la forma y hacerse una idea de la ecuación que se ajusta de
mejor manera al modelo que se busca.
Para el caso tomaremos un ejemplo
hipotético en el que se toma el esquema de una función de costos totales, donde
se sabe que hasta cierto punto en el que la producción aumenta los costos caen
dado un nivel de tecnología llegando a un mínimo y a partir de ahí existe un
incremento progresivo por cada unidad adicional por tanto se espera una forma
parabólica.
La
siguiente tabla muestra el valor del costo total Y que se obtiene con un nivel
de producción específico X.
|
|
200 |
240 |
300 |
400 |
500 |
540 |
600 |
640 |
700 |
800 |
900 |
1000 |
1040 |
1100 |
1200 |
|
y |
3910 |
3680 |
2990 |
2070 |
2070 |
1380 |
1610 |
1380 |
1725 |
1495 |
2070 |
1840 |
2530 |
2990 |
4025 |
Y
su forma gráfica es:

El
gráfico anterior muestra claramente que la tendencia no se ajusta a una recta,
esta se plantea como una curva en forma de u, siendo una parábola la ecuación que
más se ajusta es cuadrática.
En
este caso estamos tratando con una ecuación de la forma
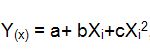
lo
que indica que tiene un valor máximo o en su defecto un mínimo.
DESARROLLO
Para
el caso de la función cuadrática es necesario aclara que es un caso espacial
que se ve en muchos ejemplos económicos, su aplicación es útil para determinar
máximos y mínimos.
El
procedimiento es el mismo que en el anterior se encuentra
![]()
Mínimo,
se deriva respecto a los coeficientes a, b y c y luego se igualan a cero, para
posteriormente simultanearlas, las ecuaciones quedan entonces:

CÁLCULO
El
siguiente paso a realizar consiste en obtener los productos y sumatorias
indicadas en las tres ecuaciones
|
|
X |
Y |
XY |
X2Y |
X2 |
X3 |
X4 |
|
|
200 |
3,910 |
782,000 |
156,400,000 |
40,000 |
8,000,000 |
1,600,000,000 |
|
|
240 |
3,680 |
883,200 |
211,968,000 |
57,600 |
13,824,000 |
3,317,760,000 |
|
|
300 |
2,990 |
897,000 |
269,100,000 |
90,000 |
27,000,000 |
8,100,000,000 |
|
|
400 |
2,070 |
828,000 |
331,200,000 |
160,000 |
64,000,000 |
25,600,000,000 |
|
|
500 |
2,070 |
1,035,000 |
517,500,000 |
250,000 |
125,000,000 |
62,500,000,000 |
|
|
540 |
1,380 |
745,200 |
402,408,000 |
291,600 |
157,464,000 |
85,030,560,000 |
|
|
600 |
1,610 |
966,000 |
579,600,000 |
360,000 |
216,000,000 |
129,600,000,000 |
|
|
640 |
1,380 |
883,200 |
565,248,000 |
409,600 |
262,144,000 |
167,772,160,000 |
|
|
700 |
1,725 |
1,207,500 |
845,250,000 |
490,000 |
343,000,000 |
240,100,000,000 |
|
|
800 |
1,495 |
1,196,000 |
956,800,000 |
640,000 |
512,000,000 |
409,600,000,000 |
|
|
900 |
2,070 |
1,863,000 |
1,676,700,000 |
810,000 |
729,000,000 |
656,100,000,000 |
|
|
1,000 |
1,840 |
1,840,000 |
1,840,000,000 |
1,000,000 |
1,000,000,000 |
1,000,000,000,000 |
|
|
1,040 |
2,530 |
2,631,200 |
2,736,448,000 |
1,081,600 |
1,124,864,000 |
1,169,858,560,000 |
|
|
1,100 |
2,990 |
3,289,000 |
3,617,900,000 |
1,210,000 |
1,331,000,000 |
1,464,100,000,000 |
|
|
1,200 |
4,025 |
4,830,000 |
5,796,000,000 |
1,440,000 |
1,728,000,000 |
2,073,600,000,000 |
|
∑ |
10,160 |
35,765 |
23,876,300 |
20,502,522,000 |
8,330,400 |
7,641,296,000 |
7,496,879,040,000 |
Con
15 observaciones se tiene un n de 15

Siguiendo el esquema anterior se procede a simultanear las
ecuaciones, comenzaremos con (1) y (2)

Simultaneando (1) y (3)
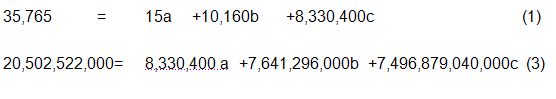
Multiplicando -8.330.400 por la (1) y 15
por la (3)
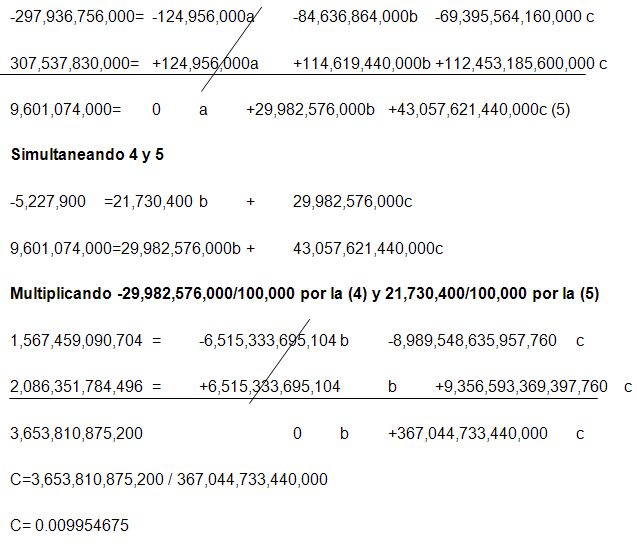
Sustituyendo
este valor en 4 y despejando b tenemos
b=
(-5,227,900 – 29,982,576,000(0.009954675))/ 21,730,400
b=
-13.97556819
Para
encontrar el coeficiente c hay que sustituir en cualquiera de (1), (2) ó (3),
tomando la ecuación primera se tiene:
35,765
= 15 a + 10,160 b + 8,330,400 c
35,765
= 15 a + 10,160 (-13.97556819) + 8,330,400 (0.009954675)
35,765
= 15 a -141991.7728 + 82926.42106
a
= (35,765+141991.7728- 82926.42106)/15
a
= 6322.023448
En
consecuencia la ecuación queda
Y(x) = 0.009954675 X2 - 13.97556819 X + 6322.023448