Fuente. Aula Fácil.2008
5. No existe correlación
entre los errores estocásticos, lo que significa que al aplicar un modelo de
regresión para perturbaciones υi de distintos puntos observados, se
obtiene un r2 cercano a cero, lo que se busca es que la estimación de “Y” no
dependa de la variación sistemática de los errores estándar la siguiente
grafica muestran la condición descrita de los errores estocásticos:
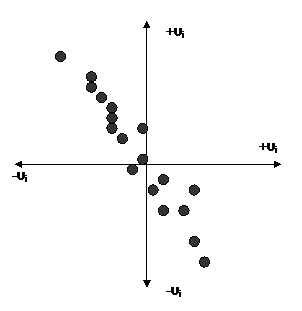
Correlación
serial Negativa, el valor de -υi es correspondido con un valor +υi y
viceversa
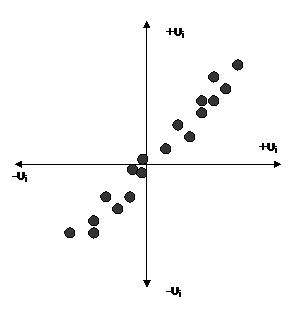
Correlación
serial Positiva, el valor de +υi es correspondido con un valor +υi y
viceversa

Correlación
cero de perturbaciones
- No existe correlación
entre los valores estocásticos y la variable independiente, en otras
palabras que no existe Covarianza entre υi y “X” o que su covarianza
es cero, al correr la variable independiente y el valor de la perturbación
se debería esperar que es cero, principalmente por que el valor de X es no
aleatorio y se asume fijo para muestras repetidas.
- El número de
observaciones debe ser mayor al número de parámetros a estimar, no
obstante no se debe olvidar que debemos contar con una serie de al menos
31 datos para ajustarse al teorema de límite central, no obstante este
criterio varia de investigador a investigador, muchos economistas apuntan
que más de 20 valores estadísticos son suficientes, también es necesario
considerar el tipo de variables que se desean estimar.
- Debe existir
variabilidad en las variables independientes, es lógico pensar este supuesto
ya que la función de regresión estimada se logra a partir de las
desviaciones entre el valor de X y el de Y, determinando de esta manera un
estimado de los parámetros, de no encontrar variabilidad, se estaría
esperando una no relación lineal entre las variables.
- Debe el modelo debe
estar especificado correctamente, es decir que lo que se plante
matemáticamente debe estar respaldado por supuestos del modelo económico y
que la forma funcional sea la que más se ajusta, finalmente se deben
incluir todas las variables involucradas que inciden en la explicación de
un fenómeno, para ello se pueden correr muchos modelos y aquellos que
demuestren un mejor nivel de correlación y de pruebas estadísticas son los
que clasifican para hacer estimaciones o demostraciones de relaciones
funcionales.
El
grado de cumplimiento de cada una de los supuestos anteriores puede variar
según el criterio del investigador, algunas pruebas que se mencionan son
determinadas automáticamente por programas computacionales, además para hacer
proyecciones a futuro se analiza la estacionariedad de la serie, el sentido de
estas pruebas esta vinculado con la variabilidad de las perturbaciones, en este
curso se presenta la prueba de significancia estadística.