El inversor se encuentra presionado por dos fuerzas opuestas:

1.- Deseabilidad de ganancias.

2.- Insatisfacción que le produce el riesgo.

1) Rentabilidad esperada, varianza y covarianza

La rentabilidad esperada es la ganancia que un inversor espera obtener de una acción en un periodo de tiempo. La rentabilidad real puede ser mayor, menor o igual.

La Varianza y desviación Standard se corresponde con la volatilidad de la rentabilidad de un titulo y se calcula de acuerdo con la desviación respecto a la rentabilidad media.

La Covarianza y Correlación supone que las rentabilidades de los títulos individuales se relacionan entre si. La covarianza es una medida estadística de la interacción de dos títulos. La interacción también se puede expresar en términos de correlación entre ellos.

La covarianza y la correlación son dos maneras de medir si dos variables (dos activos) se relacionan.

2) Rentabilidad

La fórmula generalmente aceptada para el calculo de la rentabilidad es la siguiente:

rs =ln ; Para el Indice General rm = ln; ln = Logaritmo Neperiano.

Teniendo en cuenta que en el caso de la cotización, será necesario añadir el dividendo neto percibido y el valor del derecho de ampliación cuando proceda.

Para determinar, por ejemplo, las rentabilidades anuales a partir de la rentabilidades mensuales se utilizara la siguiente formula:

rs =  - 1

siendo r1, r2, ...r12, las rentabilidades mensuales

Para periodos cortos se suele utilizar la rentabilidad continua:

Sea, por ejemplo, el calculo de la rentabilidad anual de un año determinado a partir de rentabilidades mensuales, la formula a utilizar será:

ln(1+Rn ) = = Rc

3) Riesgo de una Cartera

A u n activo financiero le podemos calcular rentabilidades diarias, semanales, mensuales y podemos formar un histograma de frecuencias de estas rentabilidades lo que conducirá a que la rentabilidad tendrá una media y una desviación standard.

La media expresara el resultado medio a esperar y la desviación standard, si tomamos las frecuencias como probabilidades, dará la probabilidad de que el valor obtenido se encuentre en un intervalo a derecha e izquierda de la media. Por esta razón la varianza, o desviación standard, mide el riesgo de un activo.

Rentabilidad y riesgo definen el activo, de tal forma que un inversor racional, entre dos activos de igual rentabilidad elegirá el de menor desviación, y entre dos activos de igual desviación el de mayor rentabilidad media.

Covarianza y Correlación

La Rentabilidad Esperada de la empresa Super es:

= 0.175 = 17.5%

Para la empresa Slow:

= 0.055 = 5.5%

Sea la siguiente información :

Super = = 0.066875

Slow = = 0.013225

que se corresponde con la varianza.

La Desviación standard = = 0.2586 = 25.86% y

= 0.1150 = 11.50%

Tenemos por lo tanto definidos las dos características de los activos, por la rentabilidad esperada y la desviación standard.

para Super 0.175% y 0.2586

para Slow 0.055 y 0.115.

Multiplicando la desviación de las dos sociedades tenemos:

= Cov(RA, RB) = = -0.004875

AB = Corr(RA, RB) =  = = -0.1629

El significado es el siguiente:

Si las dos rentabilidades de los activos se relacionan positivamente entre si, tendrán una covarianza positiva, pero si la relación que existe entre ambas es negativa, la covarianza será negativa.

Al ser en este caso la covarianza negativa = -0.004875 implica que es probable que la rentabilidad de una accion sea mayor que su promedio cuando la rentabilidad de la otra accion es menor que su promedio y viceversa. La magnitud numérica es en principio difícil de interpretar, pero se soluciona el problema mediante la Correlación.

Si la correlación es positiva, se dice que las rentabilidades se relacionan positivamente, y si es negativa, se relacionan negativamente, si es cero no se relacionan. Fluctúan por lo tanto entre +1 y -1.

4) Rentabilidad Esperada de una Cartera

X_A R_A + X _B R_B

Donde X_A y X _B son los porcentajes de inversión en los activos A y B respectivamente y R_A  y R_B   son las respectivas rentabilidades esperadas de los títulos A y B. La rentabilidad esperada de la cartera es el promedio ponderado de las rentabilidades esperadas de los activos individuales de una cartera.

Un inversor con 100 pesetas invierte 60 en la empresa Super y 40 en la Slow. La Rentabilidad esperada será:

0.6 x 17.5% + 0.4 x 5.5% = 12.7%

5) Varianza y Desviación Standard de una Cartera

Varianza : X²_AA+ 2 X_A X_BAB + X²_BB  (Dos Títulos)

En la varianza de la cartera de dos títulos se tiene en consideración la varianza de cada títulos y la covarianza de los Títulos (A con B, y B con A que son iguales)

La varianza mide la variabilidad de la rentabilidad de un titulo y la covarianza mide la relación entre dos títulos.

Una covarianza positiva entre los títulos aumenta la varianza de la cartera, mientras que una covarianza negativa disminuye la varianza de la cartera.

Para el caso de las empresas consideradas anteriormente, y teniendo en cuenta que se invierte 60 pst. en Super y un 40 en Slow, resulta:

Varianza = 0.36 x 0.066875 + 2 x (0.6 x 0.4 x (-0.004875)) + 0.16 x 0.013225. = 0.023851.

Desviación Standard :  =  = 0.1544 = 15.44%.

Una rentabilidad de -2.74% (12.7 - 15.44%) es una desviación standard menor que el promedio, y una rentabilidad del 28.14% (12.7 + 15.44) es una desviación estandard por encima del promedio. Si la rentabilidad de una cartera esta distribuida normalmente, una rentabilidad de entre -2.74 y + 28.14 % ocurre aproximadamente en un 68% de las veces.

6) Efecto de la Diversificación

El promedio ponderado de la desviación standard, para una cartera de dos títulos con las características expuestas anteriormente, es la siguiente:

0.6 x 0.2586 + 0.4 x 0.115 = 0.2012

Este resultado supone que la desviación standard de la cartera es menor que el promedio ponderado de las desviaciones standard de los títulos individuales. El motivo de esta diferencia es debido a la diversificación, ya que para las empresas Super y Slow tienen cierta correlación negativa que es:  = -0.1639, es decir, es muy probable que la rentabilidad de Super sea ligeramente menor que su media si la rentabilidad de Slow es mayor que su media y al revés.

La varianza de la cartera será:

X²_Super + 2X_Super X_{Slow Slow, Super  Slow Super}  + X²_Slow

Varianza = 0.36 x 0.066875 + 2 x 0.6 x 0.4 x (-0.1639) x 0.2586 x 0.115 + 0.16 x 0.013225. = 0.023851

Si  _{Slow Super} = 1, (Valor máximo de la Correlación), la Varianza será:

0.36 x 0.066875 + 2 x 0.6 x 0.4 x 1 x 0.2586 x 0.115 + 0.16 x 0.013225. = 0.040466.

Siendo la Desviación Standard = = 20.12

El efecto de la correlación hace disminuir la varianza cuando dicha correlación es negativa, mientras que la aumenta cuando dicha correlación es positiva.

7) Cartera Eficiente para dos Títulos:

La representación gráfica de la Rentabilidad y Desviación Standard de dos títulos es la siguiente:

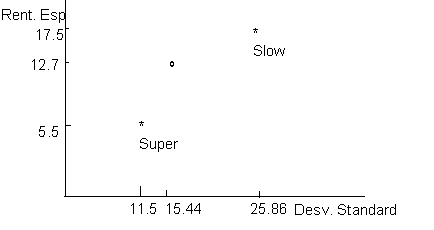
El circulo del gráfico representa una cartera con un 60% invertido en Super y un 40% en Slow. Ha de tenerse en cuenta, que es una posibilidad de la multitud de carteras que se pueden formar con los dos títulos.

En la curva del gráfico siguiente se ilustran el conjunto de carteras que se pueden formar:

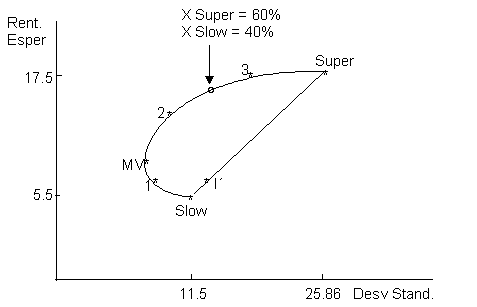
La cartera 1 esta compuesta por 90% de Slow y 10% de Super.

La cartera 2 esta compuesta al 50% para cada valor.

La cartera 3 esta compuesta al 10% en Slow y 90% Super.

La cartera MV es la cartera de varianza mínima.

Del gráfico anterior se desprenden las siguientes conclusiones:

1.- EL efecto de la diversificación se produce siempre que la correlación entre dos títulos es menor que 1, y en este caso es de 0.1639. La linea recta representa los puntos que se habrían generado si el coeficiente de correlación fuera 1. L cartera I' es una cartera con el 90% de Slow y 10% de Super con coeficiente de correlación 1, sin embargo por el efecto de la diversificación, la cartera 1 tiene la misma rentabilidad, pero menor desviación standard.

2.- El punto MV representa la cartera de varianza mínima.

3.- El inversor se enfrenta a un conjunto de oportunidades y puede situarse en cualquier punto de la curva, mediante la selección de una combinación de los dos títulos. No puede situarse en puntos superiores porque no puede incrementar la rentabilidad de los títulos individuales, reducir la desviación standard de los títulos, ni reducir la correlación de los mismos. Tampoco puede situarse en ningún punto por debajo de la curva porque no puede reducir las rentabilidades, incrementar la desviación standard, ni incrementar la correlación. Dependiendo su aversión al riesgo se situara en un punto u otro de la curva.

4.- La curva gira hacia atrás entre el punto de Slow y MV, lo que supone que la desviación standard decrece, al aumentar la rentabilidad. Esta situación es debida al efecto de la diversificación, ya que los dos títulos tienen correlación negativa entre si.

5.- Ningún inversor desea tener una cartera con rentabilidad esperada menor que la varianza mínima de la cartera. Esto supone que ningún inversor deseará la cartera I, ya que esta cartera tiene una rentabilidad esperada menor, para una desviación standard mayor que la cartera de varianza mínima. Por esta razón los inversores solo consideran la curva de MV a Super como Conjunto Eficiente.

Según sea el coeficiente de correlación, así será la forma de la curva, tal como se expresa en el siguiente gráfico:

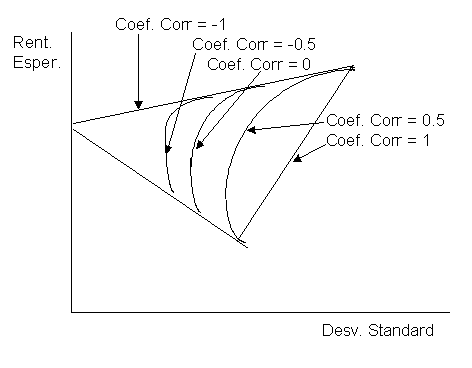
Cuanto menor es la correlación, mayor pronunciamiento de la curva, lo que implica que el efecto de la diversificación se incrementa conforme el coeficiente de correlación decrece.

8) Cartera Eficiente para muchos títulos

Sean 100 títulos que puede comprar el inversor. El conjunto de oportunidades se encuentra situado dentro de la forma sombreada de la figura siguiente:

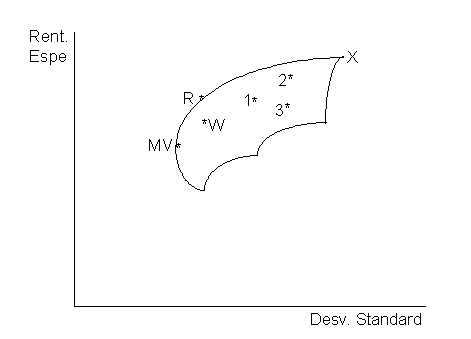
El punto 1, por ejemplo, representa una cartera de 40 títulos, el 2 de 80, el 3 de 80 pero distribuidos de forma distinta. Las combinaciones pueden ser infinitas, si bien todas entran dentro de la zona restringida. Ningún titulo o combinación de títulos puede encontrarse fuera de esa zona, lo que supone que nadie puede elegir una cartera con rentabilidad esperada mayor que la que aparece en la zona ya que no se pueden alterar las rentabilidades de los títulos individuales, y nadie puede elegir una cartera con desviación estandard menor que la que aparece en la zona, ya que no existe.

El inversor, al igual que con dos títulos, también se situara entre algún punto del extremo superior entre MV y X y que será la Cartera Eficiente. Cualquier punto por debajo de dicha cartera tendrá una rentabilidad esperada menor y la misma desviación standard, que la situada en el conjunto eficiente. Por ejemplo, R es una cartera eficiente y W estará exactamente debajo de ella. En W presenta el riesgo que desea el inversor, pero eligirá R porque la rentabilidad esperada es superior para el riesgo deseado.

9)Varianza y Desviación standard de carteras con muchos títulos

Sea N activos. Se construye una tabla que va de 1 a N en el eje horizontal y 1 a N en vertical. Esto supone una matriz de N x N = N².

10) Ejemplo:

Sean las siguientes hipótesis:

1.- Todos los títulos tienen las misma varianza = var.

2.- Todas las covarianzas son las mismas = Cov.

3.- En la cartera todos los títulos se ponderan por igual. Dado que existen N activos, el promedio ponderado de cada activo de la cartera es de 1/N, es decir Xi= 1/N para el titulo i.

Varianza de la Cartera = Nº de términos de la diagonal x Cada termino de la Diagonal + Nº de términos fuera de la diagonal x Cada termino fuera de la diagonal.

Es decir:

Varianza de la Cartera = N x (1/N²) var + N(N-1) x (1/N²)cov =

(1/N)var + ( N² - N)/N² = (1/N) + ( 1 - 1/N)cov

que en términos de tabla resulta:

Esto supone que mediante la diversificación eliminamos parte del riesgo de la cartera, pero no eliminamos la parte que corresponde a la covarianza.

La varianza de una cartera que solamente contiene un titulo es la varianza del titulo. La varianza de la cartera decrece conforme aumentan el numero de títulos, pero nuca podrá llegar a ser cero, ya que permanece la covarianza.

Gráficamente:

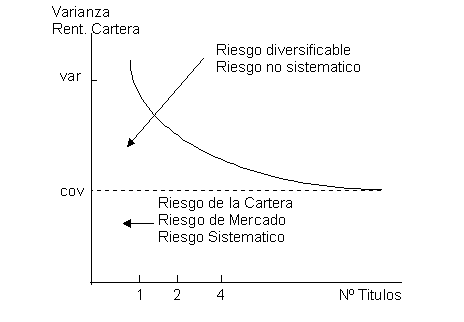
Tenemos que var > cov, por lo que la varianza de la rentabilidad de un titulo se puede descomponer de la siguiente forma:

Riesgo total de un titulo = Riesgo de la Cartera + Riesgo no Diversificable, es decir:

var = cov + (var -cov)
 

Reflexión: ¿Realmente con cuantos titulos cree es posible una elevada disminución del riesgo?